DETERMINANTES E PROPRIEDADES ADCIONAIS

Oi pessoal esse vídeo explica mais pouco sobre as propriedades dos determinantes. Ele é bem explicito sendo uma fonte de estudos para vocês.
http://youtu.be/qTnhWkEsZ6g

Pensamento: "NUNCA DESISTA DE SEUS SONHOS POR MAIS DIFÍCEIS QUE ELES SEJAM POIS UM DIA VOCÊ AINDA CHEGARÁ LÁ"

Questão do Enem 2011

Olha Pessoal mais uma questão do enem 2011 para vocês começarem a treinar para os mesmo.  Ela simples porém envolve  um interpretação da mesma.

http://youtu.be/u2Tva70XgcI

Então não vamos deixar a peteca cair. Pois o Enem está bem aí.

MATRIZES

Sei que existem muitos alunos que estão se preparando para o ENEM desse ano. Então resolvi postar aqui alguns sites e vídeos que vão esclarecer esse conteúdo tão necessário para o estudo dos educandos.

http://youtu.be/NTYUVdKZ4TQ

Vamos Pessoal é tempo de estudo. Não podemos perder o horário desse barco. Para podermos depois apreciar essa linda imagem!!!

MATRIZES

Como surgiram as matrizes

As matrizes teriam surgido com escola inglesa Trinity College, em um artigo do matemático Arthur Cayley( 1821 -1895), datado de 1858, Vale lembrar , no entanto, que, bem antes , no século III, a.C. , os chineses já desenvolviam um processo de resolução de sistemas lineares  em que implícita a idéia de matrizes.

CAYLEY criou as matrizes no contexto de extrutura algébrica  (assunto que foge aos objetivos  do ensino médio), sem pensar em suas implicações  práticas que apareceriam posteriormente.

DEFINIÇÃO

Sejam m e n números naturais não nulos

Uma matriz do tipo m x n ( ou simplesmente m x n) é uma tabela  de m.n dispostos em m linhas  (filas horizontais) e n colunas (filas verticais).

            Representamos usualmente uma matriz colocando seus elementos

( números ) entre parênteses ou entre colchetes. Menos freqüente é a  colocação entre barras  verticais à sua esquerda e duas  barras a sua direita.

Matriz de ordem m x n : Para os nossos propósitos, podemos considerar uma matriz como sendo uma tabela rectangular de números reais (ou complexos) dispostos em m linhas e n colunas. Diz-se então que a matriz tem ordem m x n (lê-se: ordem m por n) Exemplos:

A = ( 1 0 2 -4 5) ® Uma linha e cinco colunas ( matriz de ordem 1 por 5 ou 1 x 5)

B é uma matriz de quatro linhas e uma coluna, portanto de ordem 4 x 1.
Notas:

1) se m = n , então dizemos que a matriz é quadrada de ordem n.

Exemplo:


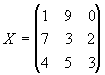
A matriz X é uma matriz quadrada de ordem 3x3 , dita simplesmente de ordem 3 .
2) Uma matriz A de ordem m x n , pode ser indicada como A = (a_ij )_mxn , onde a_ij é um elemento da linha i e coluna j da matriz.
Assim , por exemplo , na matriz X do exemplo anterior , temos a₂₃ = 2 , a₃₁ = 4 , a₃₃ = 3 , a_3,2 = 5 , etc.
3) Matriz Identidade de ordem n : I_n = ( a_ij )_{n x n} onde a_ij = 1 se i = j e a_ij = 0 se i ¹ j .

Assim a matriz identidade de 2ª ordem ou seja de ordem 2x2 ou simplesmente de ordem 2 é:

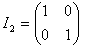
A matriz identidade de 3ª ordem ou seja de ordem 3x3 ou simplesmente de ordem 3 é:

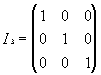
4) Transposta de um matriz A : é a matriz A^t obtida de A permutando-se as linhas pelas colunas e vice-versa.
Exemplo:

A matriz A^t é a matriz transposta da matriz A .

Notas:

4.1) se A = A^t , então dizemos que a matriz A é simétrica.

4.2) Se A = - A^t , dizemos que a matriz A é anti-simétrica.
É óbvio que as matrizes simétricas e anti-simétricas são quadradas .

4.3) sendo A uma matriz anti-simétrica , temos que A + A^t = 0 (matriz nula) .
Produto de matrizes

Para que exista o produto de duas matrizes A e B , o número de colunas de A , tem de ser igual ao número de linhas de B.
A_mxn x B_nxq = C_mxq
Observe que se a matriz A tem ordem m x n e a matriz B tem ordem n x q , a matriz produto C tem ordem m x q .
Vamos mostrar o produto de matrizes com um exemplo:

Onde L1C1 é o produto escalar dos elementos da linha 1 da 1ª matriz pelos elementos da coluna1 da segunda matriz, obtido da seguinte forma:

L1C1 = 3.2 + 1.7 = 13. Analogamente, teríamos para os outros elementos:
L1C2 = 3.0 + 1.5 = 5
L1C3 = 3.3 + 1.8 = 17
L2C1 = 2.2 + 0.7 = 4
L2C2 = 2.0 + 0.5 = 0
L2C3 = 2.3 + 0.8 = 6
L3C1 = 4.2 + 6.7 = 50
L3C2 = 4.0 + 6.5 = 30
L3C3 = 4.3 + 6.8 = 60, e, portanto, a matriz produto será igual a:

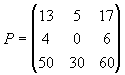
Observe que o produto de uma matriz de ordem 3x2 por outra 2x3, resultou na matriz produto P
de ordem 3x3.
Nota: O produto de matrizes é uma operação não comutativa, ou seja: A x B ¹ B x A
DETERMINANTES
Entenderemos por determinante , como sendo um número ou uma função, associado a uma matriz quadrada , calculado de acordo com regras específicas .
É importante observar , que só as matrizes quadradas possuem determinante .
Regra para o cálculo de um determinante de 2ª ordem
Dada a matriz quadrada de ordem 2 a seguir:

• O determinante de A será indicado por det(A) e calculado da seguinte forma :
• det (A) = ½ A½ = ad - bc

Exemplo:

Ora, senx.senx + cosx.cosx = sen²x + cos²x = 1 ( Relação Fundamental da Trigonometria ) . Portanto, o determinante da matriz dada é igual à unidade.
Regra para o cálculo de um determinante de 3ª ordem ( Regra de SARRUS).

SARRUS (pronuncia-se Sarrí), cujo nome completo é Pierre Frederic SARRUS (1798 - 1861), foi professor na universidade francesa de Strasbourg. A regra de SARRUS, foi provavelmente escrita no ano de 1833.
Nota: São escassas, e eu diria, inexistentes, as informações sobre o Prof. SARRUS nos livros de Matemática do segundo grau, que apresentam (ou mais simplesmente apenas citam) o nome do professor, na forma REGRA DE SARRUS, para o cálculo dos determinantes de terceira ordem. Graças ao Prof. José Porto da Silveira - da Universidade Federal do Rio Grande do Sul, pudemos disponibilizar a valiosa informação acima! O Prof. SARRUS, foi premiado pela Academia Francesa de Ciências, pela autoria de um trabalho que versava sobre as integrais múltiplas, assunto que vocês estudarão na disciplina Cálculo III, quando chegarem à Universidade. 

Para o cálculo de um determinante de 3ª ordem pela Regra de Sarrus, proceda da seguinte maneira:
1 - Reescreva abaixo da 3ª linha do determinante, a 1ª e 2ª linhas do determinante.
2 - Efetue os produtos em "diagonal" , atribuindo sinais negativos para os resultados à esquerda e sinal positivo para os resultados à direita.
3 - Efetue a soma algébrica. O resultado encontrado será o determinante associado à matriz dada.
Exemplo:

.2				3				5
.1				7				4

Portanto, o determinante procurado é o número real negativo .- 77.
Principais propriedades dos determinantes

P1) somente as matrizes quadradas possuem determinantes.

P2) o determinante de uma matriz e de sua transposta são iguais: det(A) = det( A^t ).

P3) o determinante que tem todos os elementos de uma fila iguais a zero , é nulo.
Obs: Chama-se FILA de um determinante, qualquer LINHA ou COLUNA.

P4) se trocarmos de posição duas filas paralelas de um determinante, ele muda de sinal.

P5) o determinante que tem duas filas paralelas iguais ou proporcionais, é nulo.

P6) multiplicando-se (ou dividindo-se) os elementos de uma fila por um número, o determinante fica multiplicado (ou dividido) por esse número.

P7) um determinante não se altera quando se substitui uma fila pela soma desta com uma fila paralela, multiplicada por um número real qualquer.

P8) determinante da matriz inversa : det( A^-1) = 1/det(A) .

 

Se A^-1 é a matriz inversa de A , então A . A^-1 = A^-1 . A = I_n , onde I_n é a matriz identidade de ordem n . Nestas condições , podemos afirmar que det(A.A^-1) = det(I_n) e portanto igual a 1.
Logo , podemos também escrever det(A) . det(A^-1) = 1 ;
logo , concluímos que: det(A^-1) = 1 / det(A). 
 
Notas:

1) se det(A) = 0 , não existe a matriz inversa A^-1. Dizemos então que a matriz A é SINGULAR ou NÃO INVERSÍVEL .

2) se det A ¹ 0 , então a matriz inversa A^-1 existe e é única . Dizemos então que a matriz A é INVERSÍVEL .

P9) Se todos os elementos situados de um mesmo lado da diagonal principal de uma matriz quadrada de ordem n , forem nulos (matriz triangular), o determinante é igual ao produto dos elementos da diagonal principal.

P10) Se A é matriz quadrada de ordem n e k Î R então det(k.A) = kⁿ . det A

Exemplos:

1) Qual o determinante associado à matriz?

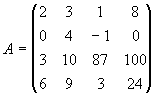
Observe que a 4ª linha da matriz é proporcional à 1ª linha (cada elemento da 4ª linha é obtido multiplicando os elementos da 1ª linha por 3). Portanto, pela propriedade P5 , o determinante da matriz dada é NULO.

2) Calcule o determinante:

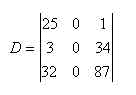
Observe que a 2ª coluna é composta por zeros; FILA NULA Þ DETERMINANTE NULO , conforme propriedade P3 acima. Logo, D = 0.

3) Calcule o determinante:

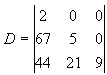
Ora, pela propriedade P9 acima, temos: D = 2.5.9 = 90

 

Exercícios propostos:

1) As matrizes A e B , quadradas de ordem 3, são tais que B = 2.At , onde A^t  é a matriz transposta de A. Se o determinante de B é igual a 40 , então o determinante da matriz inversa de A é igual a:

*a) 1/5
b) 5
c) 1/40
d) 1/20
e) 20

 

2) Seja a matriz A de ordem n onde aij = 2 para i = j e aij = 0 para i ¹ j .
Se det (3A) = 1296 , então n é igual a:
Resp: n = 4

 

3) Determine a soma dos elementos da diagonal principal da matriz A = ( aij )_{3 X 3} , onde
aij = i + j se i ³ j ou aij = i - j se i < j. Qual o determinante de A?

Resp: soma dos elementos da diagonal principal = 12 e determinante = 82

 

4) Se A = ( aij ) é matriz quadrada de ordem 3 tal que aij = i - j então podemos afirmar que o determinante da matriz 5 A é igual a:
Resp: zero

LEI DOS COSSENOS

Lei dos Cossenos: Num triângulo qualquer, o quadrado da medida de um lado é  igual a somas dos quadrados das medidas dos outros dois lados, menos duas vezes o produto das medidas desses lados  pelo cosseno do ângulo formado por eles.

Aqui ressalta que é necessário que se tenha um teodolito para calcular o ângulo exato formado pelas distâncias entre os lados do triângulo  qualquer formado . Não sendo necessariamente que esse triângulo seja um triângulo retângulo podendo ser ele acutângulo ou obtusângulo.

Bom pessoal vamos assistir o vídeo o qual fala sobre esse conteúdo.

 

http://youtu.be/nxyS9vLqJk4

Bom espero que aproveitem o conteúdo aqui postado com também apreciem essa bela vista que deixei. Essa é uma das belas praias localizada na Ilha da Gipóia  litoral sul do estado do Rio de Janeiro - Angra dos Reis.

LEI DOS SENOS

LEI DOS SENOS: Num triângulo qualquer, as medidas dos lados são proporcionais aos senos dos ângulos opostos . A razão e proporção é igual a 2R, onde R  é or raio da Circunferência circuncrita ao triângulo.

circunscrito
cir.cuns.cri.to
adj (lat circumscriptu) 1 Limitado de todos os lados por uma linha. 2 Limitado, restrito. 3 Localizado.

 Então vamos assistir ao vídeo para podermos tirarmos as nossas conclusões.

http://youtu.be/Z6l3TqLVHVI

Com o teodolito (instrumento utilizado para se medir ângulos) podemos calcular facilmente a distância que estamos de um determinado ponto a essa praia paradísica que encontra-se na Ilha grande - Angra dos Reis no Estado do Rio de Janeiro.

PORCENTAGEM COMO SE CALCULA

oi, pessoal vamos estudar um pouco mais sobre porcentagem!!..

Esse vídeo abaixo mostra claramente como se faz esse cálculo.
http://youtu.be/mg77CmgKkv8

Ele esta bem explicado para que todos usem a calculadora.

Flhttp://youtu.be/mg77CmgKn-us/images/MB900397052.jpgme de).

A CONTA DE TELEFONE E A FUNÇÃO AFIM

OI, pessoal como é  bom   estudar matemática e saber dos nossos direitos perante alguns órgões governamentais  . Então assistam o vídeo vejam como a matemática está inserida em todas questões direitos do consumidor.

http://youtu.be/DPDUdPEu-IA

Espero  gostem tirem algumas as suas dúvidas através dos comentários.

O ABASTECIMENTO DO AVIÃO E A FUNÇÃO LINEAR

Recentemente aviões com KC-135 ou Boeing 717 podem injetar 1000 galões de combustível por minuto no avião a ser abastecido.
Um avião de caça tem a capacidade de tanque com aproximadamente 5.500litros. Se ele começar o abastecimento em voo com 500 litros em seus tanques e for abastecido durante 30 segundos, podemos descrever a quantidade de combustível no tanque desse a avião em função do tempo do abastecimento.

Aqui vale lembrar que um galão equivale 3,6 litros.

3,6 litros de 1000= 3600 litros por minuto .Transformando 3600litros por minuto..
Fazendo a regra de três

3.600litros - 60segundos
x                 - 1 segundo

X = (3600 x 1) /60 = 60 litros por segundo


Então será V(s) = 60. t + 500   -   t pertence ao [ 0,30]

T(s)	V(t)
1	560
2	620
3	680
4	740
10	1100
30	2300

Então o gráfico será :

 

Sendo tipo de gráfico de função linear crescente tendo como domínio a restrição [0,30]

O PREÇO DA PASSAGEM

Pessoal  esse é mais um tipo de problema que para treinar para o ENEM

Simples e rápido   (VESTIBULAR - UFSM -RS)


Sabe-se que o preço da  a ser pago por uma corrida de táxi  inlcui uma parcela, fixa que é denominada

bandeiradas, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de

 R$4,60 e o quilômetro rodado é de R$0,96 , a distância percorrida pelo passageiro que pagou R$19,00,

para ir de sua casa  ao Shoping é de :

Traduzino para matemática:  a = R$0,96   coeficiente angular
                                            b=  R$ 4,60  coeficiente linear
                                            d = distância  a ser percorrida
                                             p(d)  = preço pago pela corrida = R$19,00

p(d)  =  a.d + b

19  =   0,96 x d  + 4,60

14,40  =  0,96 d

d =  14,4  / 0,96     =  d = 15km

REPRESENTAÇÃO GEOMÉTRICA DA EQUAÇÃO DA RETA

Vamos  determinar a função  linear  a partir do gráfico apresentado abaixo:

O gráfico abaixo representa uma função linear do tipo  y =ax +b números reais  e a diferente de zero . Então a sua representação algébrica abaixo é:

 

Olha pessoal primeiro temos que lembrar que uma função linear  é reta  representada y=ax+b

Sendo os pontos  A(0,2)   e B(3,0). Lembrando que reta faz com o eixo das abcissas um ângulo maior que 90º. Sendo a mesma decrescente. Calculando o valor de a  e b  

Y=ax +b                                    y=ax+b

2=a.0 + b                                  0 = a.3 +2

B=2                                            a=-2/3

Então a função linear ou representação algébrica será    y =-(2/3)x  +2 .  sendo  a<0