sexta-feira, 26 de setembro de 2014
quinta-feira, 25 de setembro de 2014
domingo, 7 de setembro de 2014
sexta-feira, 5 de setembro de 2014
quinta-feira, 4 de setembro de 2014
quarta-feira, 3 de setembro de 2014
segunda-feira, 1 de setembro de 2014
quinta-feira, 28 de agosto de 2014
segunda-feira, 25 de agosto de 2014
segunda-feira, 4 de agosto de 2014
terça-feira, 22 de julho de 2014
quarta-feira, 25 de junho de 2014
quinta-feira, 12 de junho de 2014
sexta-feira, 6 de junho de 2014
terça-feira, 3 de junho de 2014
sexta-feira, 30 de maio de 2014
quarta-feira, 28 de maio de 2014
terça-feira, 27 de maio de 2014
segunda-feira, 26 de maio de 2014
domingo, 25 de maio de 2014
sábado, 24 de maio de 2014
Trabalho sobre Lei dos Senos e cossenos
Trabalho do 2ºbimestre - ( Valor 3 Pontos )- Individual
1)Observe a ilustração e, com a utilização do triângulo, calcule a menor distância entre a praia e a ilha. (Valor 0,5 Ponto).
Dados sen 84º =0,99 sen21º = 0,35
Solução
A soma dos ângulos internos de qualquer triângulo é 180º
84+75+x= 180
X= 21º
Pela Le i dos Senos
x/(sen 84º)=80/(sen21º)
x/(0,99)= 80/(0,35)
x≈224m
2)Sabendo que AB = 40m , Â = 68º, e B = 75º , Indique a menor que distância o barco encalhou.(Valor 0,5 Ponto).
A soma dos ângulos internos de qualquer triângulo é 180
68+ 75+ x=180
X= 37º
A menor distância que o barco encalhou é o segmento BC
Pela Le i dos Senos
x/(sen 84º)=80/(sen21º)
x/(sen 68º)=40/(sen37º)
BC/(0,927)=40/(0,602)
BC ≈ 61,62 m ou BC ≈ 62 m
3)Dois operários conseguem manter um poste na posição vertical esticando dois cabos de aço com 50m e 70m. Se o cabo mais curto forma o ângulo de 58º com a horizontal, que distância os operários mantêm entre si?(Valor 0, 5 Ponto).
Pela Le i dos Senos
x/senβ=70/(sen58º)
sen𝛽=(50xsen58º)/70
sen𝛽= 0,6 →𝛽 = 37º
A distância d é igual. Lei dos Senos
d/sen85=70/(sen58º)
d/(0,996)=70/(0,848)
d= (70x0,996)/(0,848)
d≈82m
4)Dois lados consecutivos de um paralelogramo medem 14cm e 10cm e formam um ângulo de 60º. Calcule as medidas de suas diagonais. (Valor 0,5 Ponto).
Dados cos 60º= 1/2
O paralelogramo possui duas diagonais uma menor e outra maior.
A menor forma um ângulo 60º com os lados 10 cm 14cm
Pela Lei dos Cossenos.
Vamos calcular a diagonal menor.
X2 = 10^2 + 14^2 - 2*10*14*cos 60º
X2 = 100 +196 - 2*10*14*1/2
X2= 100 +196 – 140
X2 = 156 →X =√156 x= 2√39cm
→
Vamos calcular a diagonal maior. Lembrando que o ângulo suplementar ao de 60º é 120º
X2 = 14^2 +10^2 – 2*14*10(-cos 60)
X2 = 196 +100 + 2*14*10*1/2
X2 = 296+140
X2 = 436→x=2√109cm
5) ( = UFRJ) Os ponteiros de um relógio circular medem, do centro a extremidades, 2m o dos minutos, e 1m, o das horas. Determine a distância entre as extremidades dos ponteiros quando o relógio marca 4h. (Valor 0,5 Ponto)
Veja o esquema
Lei dos Cossenos
X2 = 2 ^2 + 1^2 - 2*2*1*(-cos60º)
X2 = 4 + 1 - 4*1/2
X2 = 4 + 1 - 2
X= √7
X≈2,67m
6) (UNICAMP- SP) A água utilizada na casa de um sítio é captada e bombeada do rio para uma caixa d’água 50m de distância. A casa está a 80m de distância da caixa d’água e o ângulo formado pelas direções caixa d’água-bomba, e o ângulo formas pelas direções caixa d’água –bomba e caixa d’água-casa é de 60º. Se se pretende bombear água do mesmo ponto de captação até a casa, quantos metros de encanamento serão necessários?( Valor 0,5 Ponto).
Pelo modo do enunciado do Problema
Esta sendo formado um triângulo é dos ãngulos é 60º . E, ele fornece os lados do mesmos sendo aplicado a lei dos Cossenos
X2 = 80^2 + 50^2 - 2* 80*50* cos 60º
X2 = 6400 + 2500 – 2*80*50 *1/2
X2 = 8.900 –4.000
X2 = 4.900
X= √(4.900)→x= 70m
quarta-feira, 14 de maio de 2014
terça-feira, 13 de maio de 2014
domingo, 11 de maio de 2014
quinta-feira, 1 de maio de 2014
terça-feira, 29 de abril de 2014
segunda-feira, 28 de abril de 2014
sábado, 26 de abril de 2014
sexta-feira, 25 de abril de 2014
Eventos Equiprováveis
Vamos estudar EVENTOS EQUIPROVÁVEIS , com esse vídeo que é bem ilustrativo.
http://youtu.be/0_PhBIUpD7w
Bons estudos.
Bons estudos.
sábado, 19 de abril de 2014
domingo, 13 de abril de 2014
sexta-feira, 11 de abril de 2014
Exercícios sobre funções Injetoras, Sobrejetoras e Bijetoras
EXERCÍCIOS RESOLVIDOS:
01 - Classifique as funções em injetora, sobrejetora ou bijetora:
a) f: R→R / f(x) = x + 2
b) f: R→R / f(x) = x²
c) f: R+→R / f(x) = x²
Resolução:
a) Bijetora
De R→R toda função do 1º grau é bijetora.
b) Sem classificação
De R→R, qualquer função quadrática não será injetora nem sobrejetora, e consequentemente não pode ser bijetora.
c) Injetora
Cuidado, neste caso, o domínio são os reais positivos, assim não teremos dois domínios resultando a mesma imagem, e sim cada domínio terá uma imagem diferente. Por fim, abaixo do eixo y, não temos nenhum ponto, tudo isso determina a função como injetora nesta definição.
I. Se f: A→B é uma função injetora, com A e B finitos então n(B) ≥ n(A), em que n(X) indica o número de elementos do conjunto X.
II. Se f: A→B é uma função sobrejetora, então todo elemento de B é imagem de pelo menos um domínio de A.
III. Toda função real de variável real que é quadrática não é injetora e nem sobrejetora.
Resolução:
I. Verdadeiro
II. Verdadeiro
III. Verdadeiro
03 - (FMJ-SP) A função f: R→B c R é definida por f(x) = x² - 6x + 5. Se essa função é sobrejetora, B pode ser indicado por:
a) ]-∞, 4[
b) [-5, 1[
c) R - [1, 5]
d) [0, 4]
e) [-4, +∞[
Resolução:
Para que a função seja sobrejetora, seu contradomínio deve ser a própria imagem da função, pois não podemos ter elementos no contradomínio que não sejam imagens de pelo menos um elemento do domínio. Dessa forma, basta encontrar a imagem da função f(x). Como essa função é quadrática, basta calcular a coordenada Y do vértice e observar a concavidade da parábola, como estudado na aula de função do 2º grau.
Yv = - (b² - 4ac)
4a
Yv = - ((-6)² - 4.1.5) / 4.1
Yv = -16 / 4
Yv = -4
Como a concavidade é voltada para cima, pois a>0, a função possui valores em y maiores que -4, logo, sua imagem que é o contradomínio B pode ser representado como [-4, +∞[
Gabarito Letra: E
Resolução:
Item III - Falso
01 - Classifique as funções em injetora, sobrejetora ou bijetora:
a) f: R→R / f(x) = x + 2
b) f: R→R / f(x) = x²
c) f: R+→R / f(x) = x²
Resolução:
a) Bijetora
De R→R toda função do 1º grau é bijetora.
b) Sem classificação
De R→R, qualquer função quadrática não será injetora nem sobrejetora, e consequentemente não pode ser bijetora.
c) Injetora
Cuidado, neste caso, o domínio são os reais positivos, assim não teremos dois domínios resultando a mesma imagem, e sim cada domínio terá uma imagem diferente. Por fim, abaixo do eixo y, não temos nenhum ponto, tudo isso determina a função como injetora nesta definição.
02 - Classifique os itens a seguir em Verdadeiros ou Falsos.
I. Se f: A→B é uma função injetora, com A e B finitos então n(B) ≥ n(A), em que n(X) indica o número de elementos do conjunto X.
II. Se f: A→B é uma função sobrejetora, então todo elemento de B é imagem de pelo menos um domínio de A.
III. Toda função real de variável real que é quadrática não é injetora e nem sobrejetora.
Resolução:
I. Verdadeiro
Se a função é injetora, o número de elementos do contradomínio deve ser maior ou igual ao número de elementos do domínio.
II. Verdadeiro
A afirmação é exatamente a definição da função sobrejetora.
III. Verdadeiro
Sempre analisamos onde a função está definida. De R→R a função do 2º grau será simples, não tem classificação.
Não será injetora pelo fato da função ser uma parábola e assim possuir uma mesma imagem para dois domínios distintos.
Pra função quadrática ser sobrejetora, depende de onde a função
está definida. Neste caso são os reais, então não será sobrejetora
pois a parábola tem um ponto máximo ou mínimo, assim sua imagem nunca
será igual ao contradomínio, nunca assume todos os valores de y
(números reais).
03 - (FMJ-SP) A função f: R→B c R é definida por f(x) = x² - 6x + 5. Se essa função é sobrejetora, B pode ser indicado por:
a) ]-∞, 4[
b) [-5, 1[
c) R - [1, 5]
d) [0, 4]
e) [-4, +∞[
Resolução:
Para que a função seja sobrejetora, seu contradomínio deve ser a própria imagem da função, pois não podemos ter elementos no contradomínio que não sejam imagens de pelo menos um elemento do domínio. Dessa forma, basta encontrar a imagem da função f(x). Como essa função é quadrática, basta calcular a coordenada Y do vértice e observar a concavidade da parábola, como estudado na aula de função do 2º grau.
Yv = - (b² - 4ac)
4a
Yv = - ((-6)² - 4.1.5) / 4.1
Yv = -16 / 4
Yv = -4
Como a concavidade é voltada para cima, pois a>0, a função possui valores em y maiores que -4, logo, sua imagem que é o contradomínio B pode ser representado como [-4, +∞[
Gabarito Letra: E
4 - (ITA 2013) Considere funções f, g, f + g : R → R. Das afirmações:
I. Se f e g são injetoras, f + g é injetora;
II. Se f e g são sobrejetoras, f + g é sobrejetora;
III. Se f e g não são injetoras, f + g não é injetora;
IV. Se f e g não são sobrejetoras, f + g não é sobrejetora,
I. Se f e g são injetoras, f + g é injetora;
II. Se f e g são sobrejetoras, f + g é sobrejetora;
III. Se f e g não são injetoras, f + g não é injetora;
IV. Se f e g não são sobrejetoras, f + g não é sobrejetora,
é (são) verdadeira(s)
A ( ) nenhuma.
B ( ) apenas I e II.
C ( ) apenas I e III.
D ( ) apenas III e IV.
E ( ) todas.
Resolução:
Item I - Falso
Podemos ter a função constante, que não é injetora.
Seja f = x e g = -x (as duas injetoras)
f + g = 0 (função constante)
Item II - Falso
Mesmo motivo do item anterior, a função constante não é sobrejetora.
Seja f = x e g = -x (as duas sobrejetoras)
f + g = 0 (função constante)
Item III - Falso
Seja f = x² + 2x + 1 e g = -x² - x, ambas não injetoras, temos:
f + g = x + 1, que é injetora.
Item IV
Falso, seja f = x² + x e g = -x² + 1, ambas não sobrejetoras,
f + g = x + 1, sobrejetora.
Gabarito Letra: A
quarta-feira, 9 de abril de 2014
Funções Injetoras,Sobrejetoras e Bijetoras
Depois de conhecermos o conceito de função, estudaremos agora como classificá-las.
Se você não sabe do que se tratam os símbolos D(f), CD(f) e Im(f), convém revisar a simbologia utilizada ao trabalharmos com funções, ela será necessária para uma boa compreensão desta matéria.
Estudaremos os três tipos de função que são: Sobrejetora, injetora e bijetora.
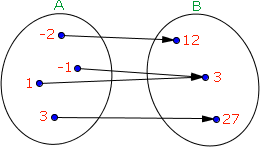 Vamos analisar o diagrama de flechas ao lado:
Vamos analisar o diagrama de flechas ao lado:
Como sabemos o conjunto A é o domínio da função e o conjunto B é o seu contradomínio.
É do nosso conhecimento que o conjunto imagem é o conjunto formado por todos os elementos do contradomínio que estão associados a pelo menos um elemento do domínio e neste nosso exemplo, todos os elementos de B estão associados a pelo menos um elemento de A, logo nesta função o contradomínio é igual ao conjunto imagem.
Classificamos como sobrejetora as funções que possuem o contradomínio igual ao conjunto imagem.
Note que em uma função sobrejetora não existem elementos no contradomínio que não estão flechados por algum elemento do domínio.
Nesta função de exemplo temos:
Domínio: D(f) = { -2, -1, 1, 3 }
Contradomínio: CD(f) = { 12, 3, 27 }
Conjunto Imagem: Im(f) = { 12, 3, 27 }
Esta função é definida por:
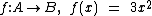
Substituindo a variável independente x, de 3x2, por qualquer elemento de A, iremos obter o elemento de B ao qual ele está associado, isto é, obteremos f(x).
Do que será explicado a seguir, poderemos concluir que embora esta função seja sobrejetora, ela não é uma função injetora.
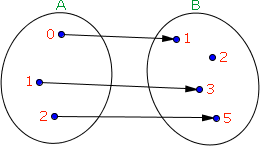 Vejamos agora este outro diagrama de flechas:
Vejamos agora este outro diagrama de flechas:
Podemos notar que nem todos os elementos de B estão associados aos elementos de A, isto é, nesta função o conjunto imagem difere do contradomínio, portanto esta não é uma função sobrejetora.
Além disto podemos notar que esta função tem uma outra característica distinta da função anterior.
Veja que não há nenhum elemento em B que está associado a mais de um elemento de A, ou seja, não há em B qualquer elemento com mais de uma flechada. Em outras palavras não há mais de um elemento distinto de A com a mesma imagem em B.
Nesta função temos:
Domínio: D(f) = { 0, 1, 2 }
Contradomínio: CD(f) = { 1, 2, 3, 5 }
Conjunto Imagem: Im(f) = { 1, 3, 5 }
Definimos esta função por:
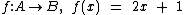
Veja que não há no D(f) qualquer elemento que substituindo x em 2x + 1, nos permita obter o elemento 2 do CD(f), isto é, o elemento 2 do CD(f) não é elemento da Im(f).
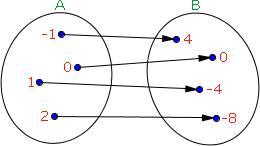 Na explicação do último tipo de função vamos analisar este outro diagrama de flechas:
Na explicação do último tipo de função vamos analisar este outro diagrama de flechas:
Do explicado até aqui concluímos que este é o diagrama de uma função sobrejetora, pois não há elementos em B que não foram flechados.
Concluímos também que esta é uma função injetora, já que todos os elementos de B recebem uma única flechada.
Esta função tem:
Domínio: D(f) = { -1, 0, 1, 2 }
Contradomínio: CD(f) = { 4, 0, -4, -8 }
Conjunto Imagem: Im(f) = { 4, 0, -4, -8 }
Esta função é definida por:
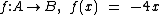
Ao substituirmos x em -4x, por cada um dos elementos de A, iremos encontrar os respectivos elementos de B, sem que sobrem elementos em CD(f) e sem que haja mais de um elemento do D(f) com a mesma Im(f).
Funções que como esta são tanto sobrejetora, quanto injetora, são classificadas como funções bijetoras.
Se você não sabe do que se tratam os símbolos D(f), CD(f) e Im(f), convém revisar a simbologia utilizada ao trabalharmos com funções, ela será necessária para uma boa compreensão desta matéria.
Estudaremos os três tipos de função que são: Sobrejetora, injetora e bijetora.
Função Sobrejetora
 Vamos analisar o diagrama de flechas ao lado:
Vamos analisar o diagrama de flechas ao lado:Como sabemos o conjunto A é o domínio da função e o conjunto B é o seu contradomínio.
É do nosso conhecimento que o conjunto imagem é o conjunto formado por todos os elementos do contradomínio que estão associados a pelo menos um elemento do domínio e neste nosso exemplo, todos os elementos de B estão associados a pelo menos um elemento de A, logo nesta função o contradomínio é igual ao conjunto imagem.
Classificamos como sobrejetora as funções que possuem o contradomínio igual ao conjunto imagem.
Note que em uma função sobrejetora não existem elementos no contradomínio que não estão flechados por algum elemento do domínio.
Nesta função de exemplo temos:
Domínio: D(f) = { -2, -1, 1, 3 }
Contradomínio: CD(f) = { 12, 3, 27 }
Conjunto Imagem: Im(f) = { 12, 3, 27 }
Esta função é definida por:
Substituindo a variável independente x, de 3x2, por qualquer elemento de A, iremos obter o elemento de B ao qual ele está associado, isto é, obteremos f(x).
Do que será explicado a seguir, poderemos concluir que embora esta função seja sobrejetora, ela não é uma função injetora.
Função Injetora
 Vejamos agora este outro diagrama de flechas:
Vejamos agora este outro diagrama de flechas:Podemos notar que nem todos os elementos de B estão associados aos elementos de A, isto é, nesta função o conjunto imagem difere do contradomínio, portanto esta não é uma função sobrejetora.
Além disto podemos notar que esta função tem uma outra característica distinta da função anterior.
Veja que não há nenhum elemento em B que está associado a mais de um elemento de A, ou seja, não há em B qualquer elemento com mais de uma flechada. Em outras palavras não há mais de um elemento distinto de A com a mesma imagem em B.
Nesta função temos:
Domínio: D(f) = { 0, 1, 2 }
Contradomínio: CD(f) = { 1, 2, 3, 5 }
Conjunto Imagem: Im(f) = { 1, 3, 5 }
Definimos esta função por:
Veja que não há no D(f) qualquer elemento que substituindo x em 2x + 1, nos permita obter o elemento 2 do CD(f), isto é, o elemento 2 do CD(f) não é elemento da Im(f).
Função Bijetora
 Na explicação do último tipo de função vamos analisar este outro diagrama de flechas:
Na explicação do último tipo de função vamos analisar este outro diagrama de flechas:Do explicado até aqui concluímos que este é o diagrama de uma função sobrejetora, pois não há elementos em B que não foram flechados.
Concluímos também que esta é uma função injetora, já que todos os elementos de B recebem uma única flechada.
Esta função tem:
Domínio: D(f) = { -1, 0, 1, 2 }
Contradomínio: CD(f) = { 4, 0, -4, -8 }
Conjunto Imagem: Im(f) = { 4, 0, -4, -8 }
Esta função é definida por:
Ao substituirmos x em -4x, por cada um dos elementos de A, iremos encontrar os respectivos elementos de B, sem que sobrem elementos em CD(f) e sem que haja mais de um elemento do D(f) com a mesma Im(f).
Funções que como esta são tanto sobrejetora, quanto injetora, são classificadas como funções bijetoras.
domingo, 30 de março de 2014
sábado, 29 de março de 2014
quinta-feira, 27 de março de 2014
quarta-feira, 26 de março de 2014
terça-feira, 25 de março de 2014
domingo, 23 de março de 2014
Assinar:
Postagens (Atom)